And I'm Dan, a Commander player who is obsessed with building thematic decks. I connect the stories to Magic cards to create decks that reflect the vibrant tales of the past.

We take famous or not-so-famous figures from history and make Commander decks based on their lives, philosophies, and histories.

Our articles are meant to be part history lesson, part deckbuilding guide. We believe that decks can be expressions of personal philosophies, so a fun way to learn about historical figures -- and flavorful brews -- would be to speculate about what sort of Commander deck a given person would play, given their times, opinions, and philosophies.

It's like a history class, only using the medium of Magic: the Gathering.

This is meant to be an accessible glimpse at the people in question, not a rigorous or definitive biography; we have sources at the end of the article for that!

Let us begin!

Who Was Srinivasa Ramanujan?

Srinivasa Ramanujan (1887 - 1920) was an Indian mathematician and theorist whose work has been used in everything from examining black holes to trying to understand the patterns of how cancer spreads. Despite having little formal training, Ramanujan made many groundbreaking discoveries that have influenced the world of mathematics to this day.

Ramanujan had an incredible intuition for numbers and formulae; many of his discoveries, he said, we revealed to him in dreams and visions from the goddess Namagiri Thayar. Magic's own God of inspiration is Keranos, and we think Ramanujan would have appreciated Keranos's mechanical representation of divine inspiration.

Early Life and Relationship to Mathematics (1887-1903)

Srinivasa Ramanujan was born in Erode, in modern day Chennai (formerly Madras, in South India) to an orthodox Brahmin-caste Hindu family. He had a somewhat difficult childhood; while his family was high-caste, they were not especially well off financially. Ramanujan seemed a normal enough child until he stumbled upon pure mathematics.

As many beautiful things begin, this sequence begins with a book. Specifically, a book titled A Synopsis of Elementary Results in Pure and Applied Mathematics by Carr. It was a book about pure mathematics, which immediately hooked Ramanujan. It was a fine book, to be sure, but it didn't describe the methods for reaching conclusions, leaving Ramanujan to develop his own--highly original--means of reaching them.¹

Once Ramanujan discovered pure mathematics, he could not be easily persuaded to pay attention to much else in his studies; history, economics, etc., left him cold.

Ramanujan made mathematics and his study a part of his being. Mathematics became not just another language, but practically another sense for Ramanujan, something that he took into himself and was as much shaped by his personality as it was an expression of sublime beauty. Pure mathematics got into his bloodstream, the marrow of his bones; it assumed a not-inconsiderable spiritual element inside Ramanujan's life. He is credited as saying: "An equation for me has no meaning unless it expresses a thought of God."

He dreamed about equations, felt that the gods made themselves known to him, subconsciously and consciously, through this language of letters and numbers.² Ramanujan's divine visions are represented in his deck with scry and similar abilities, getting him just the information he needs at any time and setting up Keranos's trigger. There's a heavy instant and sorcery theme in this deck, so Spite of Mogis is a cheap and powerful removal spell, while Zaffai, Thunder Conductor and Jace's Sanctum can trigger almost every turn. All that scrying can also help set up powerful miracle spells, like Bonfire of the Damned and Temporal Mastery, which also nicely demonstrate the flavor of divine intervention.

Ramanujan first began to keep notebooks full of his theorems and mathematical explorations in 1907. He would continue this habit of keeping notebooks full of pure mathematical wanderings (formulas, problems, musings) until the year of his death, 1920.

According to one his biographers: "Ramanujan was an artist. And numbers--and the mathematical relationships they represented--were his medium."

Leaving India (1914)

Seven years after Ramanujan first began to keep notebooks and seriously apply himself to pure math, he left India for England. During this time, he had been somewhat adrift, making a little money from tutoring, but largely losing himself in his study and adaptation of pure mathematics. He was married by that time, but this did not dissuade his pursuit of math.

Ramanujan had exhausted all of the mathematicians in his part of India during this rootless time in his life, so he, at the urging of his friends and acquaintances, took up correspondence with the already-famous British mathematician G.H. Hardy.³

Hardy was so impressed with Ramanujan's mathematical skills that he replied, and the two became pen pals. Eventually, that admiration (and Hardy's repeated boosting of Ramanujan's work which greatly helped accelerate his career) led to an invitation for Ramanujan to come to Trinity College in England, the place to be for higher level math at the time.

There was a problem, though: Brahmin-caste people like Ramanujan weren't supposed to travel across the oceans; to do so at that time risked becoming an outcast⁴, which meant that one's life was effectively over. Ramanujan was between a rock and a hard place.

So, in response to this dilemma, Ramanujan undertook a pilgrimage with his mother and a few friends to Nammakal to visit the temple of Namagiri. Ramanujan and his companions slept for three nights on the temple grounds--on the third night, Ramanujan bolted up from sleep and declared joyously that Namagiri had waived the travel prohibitions for Brahmins in his case--he could go to England after all!⁵

Partnership with Hardy in England (1914-1919)

Hardy, the "Apostle of Proofs", demanded that the intuitive and brilliant leaps that Ramanujan made, and that seemed so self-evident to him, be made visible. Showing his work, in other words. It is difficult to boil down things that one has come to understand through study and intuition into language, let alone one as precise and distinct as mathematical notations. Hardy once wrote, in a letter to Ramanujan, "I want particularly to see your proofs of your assertions here. You will understand that, in this theory, everything depends on rigorous exactitude of proof."

Ramanujan wanting to publish his conclusions without rigorous proofs was akin to a Magic player wanting to cast spells without paying their mana costs, though the latter works out better for him in this deck. Just as Namagiri showed Ramanujan formulae in his dreams, Keranos lets him cast Deflecting Swat and Fierce Guardianship for free. As Foretold, Wild Evocation, and Plargg and Nassari cast free spells turn after turn. The demonstrate ability on Creative Technique suggests the collaboration between Ramanujan and Hardy. After casting several free spells in a turn, Mind's Desire can power out several more, reflecting Ramanujan's fervent output. Fortunately for mathematical posterity, Hardy nixed Ramanujan's freewheeling ways, getting him to slow down and write out his proofs.

Despite their differences, Hardy and Ramanujan became close friends and associates. Hardy was awestruck by Ramanujan's "invincible originality," as he would later write for the great mathematician's obituary. Hardy wanted to encourage Ramanujan to learn to use formal mathematical proofs more consistently (so that he would have to be accepted by the notoriously hidebound British mathematical establishment) without dampening the younger man's passionate love for discovery or for math, a tension that was difficult to navigate at times.

His biographer, Kanigel, once wrote, "While the mathematical tools Ramanujan used were subtle and powerful, the problems to which he applied them were often surprisingly easy to formulate."

The two men's friendship was cemented by mutual respect and fluency in math and rapidly eclipsed quantifiable categories. This has puzzled some people: Hardy was a militant atheist, Ramanujan a devout Hindu; Hardy demanded the quantifiable, Ramanujan reached quantifiable results through intuitive (though, I cannot emphasize this enough, studied) means.

Different they might have been, they seemed to revel in how the other saw the world and were more intrigued (and shaped) by the other.

They were mathematician-bros, to be crude about it.

A Quick Word on Partitions

Ramanujan's mathematical accomplishments were many and varied, but one we can explain in this space is the matter of partitions. In Magic terms, the question can be stated thusly: for a given value of X, how many different ways can you split up the damage for Rolling Thunder? Mathematicians call a specific way of dividing the damage a partition, and use the term p(X) to denote the number of possible partitions of X damage.⁶

For small values of X, this is easy to work out by hand. For example, here are the five ways that 4 damage can be divided:

However, the number of possibilities increases very quickly as X increases. When X is 10, there are 42 ways to split the damage. By the time X reaches 100, it's shot up to 190,569,292. For values of X this large and larger, enumerating the possibilities becomes prohibitively onerous.

Despite the apparent simplicity of the question, a general formula for partitions long eluded mathematicians. Hardy's Trinity College colleague, Major MacMahon, calculated by hand the values of p(X) at least up to X=200, but he believed that no formula would ever be found. Ramanujan was determined to prove otherwise, and, working with Hardy, discovered this approximation formula for the number of possible partitions in 1918:

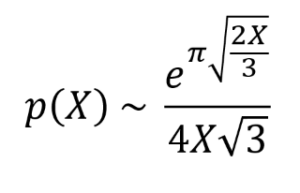
The tilde (~) here means approximately equal to, and indicates that the approximation gets closer to the true value as X increases. If you're not familiar with mathematical notation, this formula probably looks rather intimidating; however, it is actually straightforward to replace both the Xs with the value of your choice, plug the formula into your calculator, and get out the answer. Putting in 100 for X, we get an approximation of 199,280,893, which is only 4.6% over the actual number of partitions.

The moral of this story is that if an opponent ever casts Rolling Thunder with X=100, forgive them if they take a while dividing up the damage: they have nearly 200 million possible choices to consider!

Rolling Thunder is the poster child for damage division in Magic, but there are many similar effects Ramanujan included in his EDH deck as well. Meteor Shower and Conflagrate are more expensive backups, and Magmatic Core lets him go through the whole p(X) sequence, starting at p(0). There are also spells with the value of X fixed anywhere from 2 up to 8, as well as 10:

Ramanujan and Hardy in fact found a formula for the exact value of p(X), though that is beyond the scope of this article. The approximation formula shown above is only the first of many terms in that formula. If you wish to learn more, you can find Ramanujan and Hardy's paper introducing the formula here.

Success in England... At a Cost

Ramanujan ultimately was highly lauded in England. In 1917, he was voted into the London Mathematical Society. The following year, he was elected into the Royal Society before finally becoming a Fellow at Trinity College. All of these were high honors to bestow on an Indian at the peak of the brutally racist and imperialist British empire.

But such things came at high personal cost to Ramanujan: he was frequently cold, sick, and miserable.⁸ Besides the native hostility of the British academic upper class, Ramanujan had other problems. He was a strict vegetarian in a country where almost everything was prepared with some animal product or other, in the middle of the First World War so heavy rationing was even further limiting his caloric options. He frequently lost weight and was ill, things that hardly could have helped any.

Ramanujan eventually returned to India having somewhat recovered his health, before taking ill and dying in 1920. He was thirty-two years old, but he had changed mathematics forever.

Afterlife: Ramanujan's Lost Notebooks (1976)

Of course, for someone as prolific as Ramanujan, the fallout of his death was not evenly distributed. Letters, notebooks, and notes from him popped up for years after his death (some curated by his family), but the most notorious of these was the accidental stumbling across of his lost notebooks.

They were discovered by George Andrews, a professor at the University of Wisconsin, in the house of the deceased G.N. Watson during a trip to Europe.  Here's the bullet-point version of events:

• G.N. Watson was an accomplished mathematician, but frustratingly also kept every paper document he ever came into contact with, making the fact that George Andrews managed to "dip" out Ramanujan's papers from the paper-storm a minor miracle, even more so when one considers the fact that the papers were due to be incinerated in the next few days.
• Part of the reason the 'Lost Notebooks' had gone undiscovered as containing new information written by Ramanujan was that the people in possession with the papers were familiar with Ramanujan's work generally and assumed they contained nothing new. Watson had just finished a Ph.D. on the field that some of the theorems applied to (mock theta functions) and immediately realized that these were letters that could only have been written during Ramanujan's final years and represented an entirely new approach.
• "Providential"/"miraculous" doesn't begin to cover how fortunate this discovery was. Ramanujan's work, both formal and from the "lost notebooks", reshaped multiple fields outside pure mathematics: biology, astronomy, cancer research, to name but three. Or as his biographer put it: "The great tree that was Ramanujan's work sent its roots down deep and far."

Just as later mathematicians and scientists look to his lost notebooks for inspiration, Ramanujan's Commander deck looks to its graveyard to close out the game. Inferno Project, Haughty Djinn, and Serpentine Curve (appropriately from the mathematical college of Quandrix) all provide plenty of power after a game full of instant and sorcery spells. Alternatively, Wondrous Crucible and Arcane Bombardment can bring those spells back for another round. Maybe he could even get an infinite turns combo going with Arcane Bombardment and Time Stretch; a bittersweet contrast to his own too-short life.

Srinivasa Ramanujan's full Commander decklist is below!

The Prince of Intuition: Srinivasa Ramanujan's EDH Deck

View on Archidekt

---

Commander (1) 1 Keranos, God of Storms Instants (15) 1 Chandra's Pyrohelix 1 Deflecting Swat 1 Electrolyze 1 Fierce Guardianship 1 Force of Negation 1 Force of Will 1 Gush 1 Intuition 1 Magma Opus 1 Misdirection 1 Nix 1 Pyrokinesis 1 Spreading Flames 1 Submerge 1 Twin Bolt Sorceries (22) 1 Aminatou's Augury 1 Arc Lightning 1 Beacon of Tomorrows 1 Bonfire of the Damned 1 Conflagrate 1 Creative Technique 1 Devastation Tide 1 Experimental Overload 1 Fight with Fire 1 Meteor Shower 1 Meteor Swarm 1 Mind's Desire 1 Pyrotechnics 1 Rolling Thunder 1 Serpentine Curve 1 Serum Visions 1 Spite of Mogis 1 Sundering Stroke 1 Temporal Mastery 1 Time Stretch 1 Volcanic Wind 1 Volley of Boulders Enchantments (8) 1 Arcane Bombardment 1 As Foretold 1 Jace's Sanctum 1 Magmatic Core 1 Omniscience 1 One with the Multiverse 1 Sunbird's Invocation 1 Wild Evocation Creatures (15) 1 Bogardan Hellkite 1 Fury 1 Galvanoth 1 Haughty Djinn 1 Inferno Project 1 Inferno Titan 1 Octavia, Living Thesis 1 Plargg and Nassari 1 Prognostic Sphinx 1 Sapphire Dragon // Psionic Pulse 1 Serum Sovereign 1 Spellheart Chimera 1 Thassa, God of the Sea 1 Wildfire Eternal 1 Zaffai, Thunder Conductor Lands (37) 1 Castle Vantress 1 Crystal Grotto 13 Island 14 Mountain 1 Path of Ancestry 1 Prismari Campus 1 Rivendell 1 Spinerock Knoll 1 Spirebluff Canal 1 Steam Vents 1 Temple of Epiphany 1 Zhalfirin Void Artifacts (1) 1 Wondrous Crucible Planeswalkers (1) 1 Ral, Storm Conduit

1. "A western mathematician who knew Ramanujan's work would later observe that Synopsis had given him direction, but had 'nothing to do with his methods, the most important of which were completely original.'" Kanigel, p.45
2. Ramanujan once reported that he had had a dream of a divine hand tracing out elliptical integrals on a bloody red screen and watched with rapt attention.
3. Hardy was actually the third English Mathematician that Ramanujan wrote to; the other two, reflecting the manifold prejudices of the time and empire, didn't deign to reply to Ramanujan's earnest letters. Hardy is a character in and of himself; Kanigel devotes about a fourth of his biography of Ramanujan to Hardy, who called his relationship with Ramanujan "the one romantic incident of my life". After Ramanujan's death, Hardy didn't forget his old friend and made sure his work was given credit--not that he was idle either. A staunch anti-militarist, a position that had cost him during the First World War, he helped find jobs for European Jews fleeing persecution in the lead up to and during WWII and whose new years resolution list once included three items like: "1. Prove the Riemann hypothesis 2. Find a proof for the nonexistence of God that should convince the general public and 3. Murder Mussolini." He also was a huge fan of baseball problems and the sport in general, unusual for the British upper crust.
4. "For an orthodox Hindu--and Ramanujan came from a very Orthodox Hindu family--traveling to Europe or America represented a form of pollution...and traditionally, it had the same outcome [for breaking the tradition]--exclusion from caste. That meant your friends and relatives would not have you to their homes. You could find no bride or bridegroom for your child...sometimes you couldn't go into temples...here was the grim day-to-day meaning of the word outcaste." -Robert Kanigel, The Man Who Knew Infinity
5. Some accounts of this event have the ecstatic dream happening only to Ramanujan's mother, or to them both. For simplicity, I've condensed it to just Ramanujan, since my source for this incident, The Man Who Knew Infinity by Kanigel, admits that the exact scenario at Nammakal is pretty much impossible to verify the specifics of with certainty.
6. Throughout this section, we assume that there are at least X targets available, and that they are all functionally identical. Distinguishing between the targets would add a further layer of complication.
7. Sundering Stroke is not an ideal example, since it can only hit up to three targets; it's just the only spell that divides 7 damage.
8. According to Kanigel, a fellow Indian who visited Ramanujan at Trinity in 1914, he saw that Ramanujan was shivering in the English winter and slept in a overcoat and shawl.  Was Ramanujan getting enough blankets? Ramanujan showed him his sleeping quarters, and there as a stack of blankets undisturbed: his comrade had to show him how to use them to stay warm (coming from southern India, it was very possible that Ramanujan had never had a need for heavy blankets or had any way of preparing for the English cold and damp.