What Would They Play? Leonhard Euler's EDH Deck
Welcome to What Would They Play?
And I'm Dan, a Commander player who is obsessed with building thematic decks. I connect the stories to Magic cards to create decks that reflect the vibrant tales of the past.
We take famous or not-so-famous figures from history and make Commander decks based on their lives, philosophies, and histories.
Our articles are meant to be part history lesson, part deckbuilding guide. We believe that decks can be expressions of personal philosophies, so a fun way to learn about historical figures -- and flavorful brews -- would be to speculate about what sort of Commander deck a given person would play, given their times, opinions, and philosophies.
It's like a history class, only using the medium of Magic: the Gathering.
This is meant to be an accessible glimpse at the people in question, not a rigorous or definitive biography; we have sources at the end of the article for that!
Let us begin!
Who Was Leonhard Euler?
The nicest mathematician us non-math nerds haven't heard of, Leonhard Euler (pronounced 'Oiler', not 'Ewe-ler') was born in 1707 in Basel, Switzerland.
You can't throw a rock in pure or applied mathematics without hitting something that Euler wrote, invented, or theorized. Here's a short list of his accomplishments so we don't have to mention them later in the article; for further reading on Euler, we recommend this short biography by Walter Gautshi.
- Pivotal in development of partition theory (for more on that, and on Ramanujan, the Indian 20th century mathematician who took the form to its highest level, see our article on him and what he would play in Commander here).
- He single-handedly created the field of graph theory, for one thing, which will be relevant in this article as we discuss traveling, the use of math to understand relations between places and movement.
Also, the sheer number of things named after Euler is staggering, though my favorite is the Euler Disc. One of the most significant, however, is Euler's number, which is approximately equal to 2.71828; mathematicians since Euler's time have denoted this number with the letter e. The applications of this number are in exponential growth, where a number is repeatedly multiplied by the same constant. The card Exponential Growth is, in fact, a perfect demonstration of the concept. To extend this to a whole deck theme, Euler's deck is built around Xenagos, God of Revels as the commander; with one doubling effect in the command zone and many others in the deck, he's ready to unleash the power of exponential growth upon his opponents.
Early Life
Leonhard Euler was born into a Swiss Protestant family.1 He entered a local university at 13 and was swiftly recognized as having an exceptional talent for mathematics, even though he initially entered to study theology. His mathematical genius, however, meant that he was encouraged away from the clergy, so he dedicated himself to mathematics.
Euler himself describes his six years of education as follows in his autobiography:
"In 1720 I was admitted to the university as a public student, where I soon found the opportunity to become acquainted with the famous professor Johann Bernoulli, who made it a special pleasure for himself to help me along in the mathematical sciences. Private lessons, however, he categorically ruled out because of his busy schedule. However, he gave me a far more beneficial advice, which consisted in myself getting ahold [sic] of some of the more difficult mathematical books and working through them with great diligence, and should I encounter some objections or difficulties, he offered me free access to him every Saturday afternoon, and he was gracious enough to comment on the collected difficulties, which was done with such a desired advantage that, when he resolved one of my objections, ten others at once disappeared, which certainly is the best method of making happy progress in the mathematical sciences."
It was actually Bernoulli's older brother, Jacob, who first calculated the value of the number e, while studying compound interest. Euler was the first to use the letter e to denote it (choosing e for exponent, not for Euler), as well as proving it is an irrational number (i.e., it can't be written as a fraction of two whole numbers) and proving this derivation of the number:
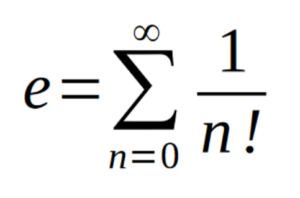
This formula is an infinite sum that starts out like this:
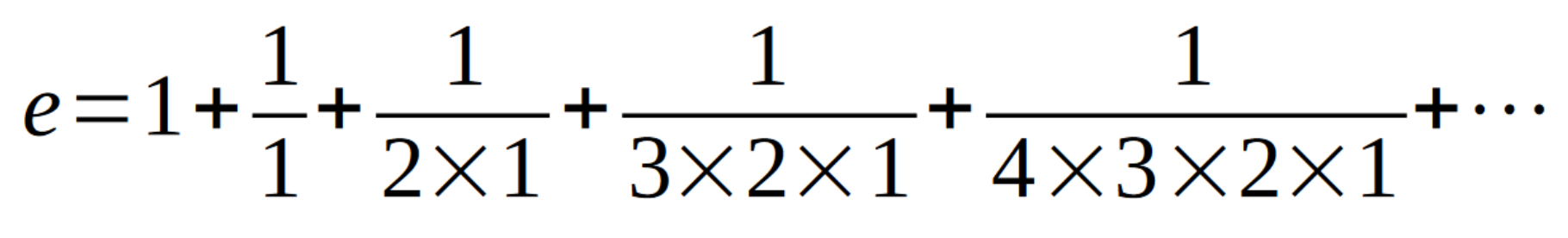
Clearly the man was interested in exponential growth. Red and green offer plenty of ways to double damage or a creature's power; deploying a few of these at once results in exponential growth that can turn an insignificant creature into a game-ending threat. Kalonian Hydra and Primordial Hydra grow exponentially over multiple turns. For a burst of growth, Berserk, Unleash Fury, and Neyith of the Dire Hunt could all be deployed in one turn. Utvara Hellkite, Scute Swarm, and Horn of Gondor exponentially grow an army of Dragons, Scute Swarms, and Human Soldiers, respectively; try combining them with Devilish Valet for exponential growth on two axes.
Traveling Mathematician
Leonhard Euler ultimately made a living as a 'court mathematician'; that is, traveling through Europe, taking patronage from the local (or national) upper classes, and dedicating oneself to study. Most notably, he served in the courts of Frederick II (the Great) and Catherine II (the Great, though of Russia although she was born in what is now Germany)2
As Gautshi notes, Euler's travels could be broken roughly into four stages:
- Basel, Switzerland (1707-1727)
- St. Petersburg (1727-1741, this is where Euler burst onto the world mathematical stage in earnest)
- Berlin (1741-1766)
- St. Petersburg(again! 1766-1783)
But throughout those roughly 20-year stints, Euler made the best of frequently less-than-ideal situations. His work was very much catch-as-catch-can; when one thinks of a court mathematician, one's imagination might run away with them. Luxurious rooms, lots of time alone to theorize, peace, quiet, graph paper. Maybe the cry of a passing gull or robin in the background. Not so for Euler. He made do with what he could get in terms of uninterrupted time (or interrupted time). One of his peers during his time in Frederick II's Berlin, Thibault quipped:
"A child on the knees, a cat on his back, that's how he [Euler] wrote his immortal works."
He had the supreme gift of being able to inhabit a physical and abstracted interior world at once.
Even more atypical in the cutthroat level of courtiers and academics was Euler's magnanimity and willingness to share with others in his field(s). Gautshi notes:
"Sharing ideas with others and letting others take part in the process of discovery is another noble trait of Euler. A case in point is the way he put on hold his already extensive work on hydrodynamics, so that his friend Daniel Bernoulli, who was working on the same topic, could complete and publish his own Hydrodynamics first! It became a classic."
Euler is similarly happy to help out other players in a game of Commander. With Tahngarth, First Mate and Assault Suit, he can contribute his creatures to another player's attack. Hithlain Rope, Bucknard's Everfull Purse, and Humble Defector can get passed around the table to the benefit of all.
The Seven Bridges of Königsberg (1736)
One famous problem Euler solved was called The Seven Bridges of Königsberg. In the 1700s, there were seven bridges in that city connecting the two banks of the river Pregel (now called Pregolya) and two islands in the river. A popular unsolved puzzle was to find a path through the city that crossed each of the seven bridges exactly once--no doubling back, and no crossing the river by any other means.
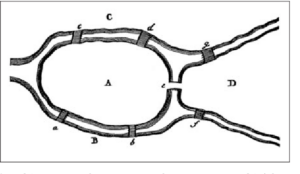
If you're a Magic story fan, this problem may seem familiar: in Dragon's Maze, the guilds of Ravnica raced to find a secret path through the city's ten guildgates to earn a prize of great power. Other than featuring ten gates rather than seven bridges, the Implicit Maze differs from the bridges of Königsberg in one significant way: while Jace Beleren found his way through the Maze and became the Living Guildpact, Euler instead proved that there is no way to cross all seven bridges without repeating one. Perhaps this conclusion is not satisfying enough for a fantasy novella, but in proving it Euler invented the field of graph theory, which today finds applications in everything from cartography to computer networks.
The Gruul color identity of Euler's deck only allows him access to nine Gates, so he's not going for a Maze's End victory here. Nevertheless, having a few Gates out can provide some nice bonuses with Heap Gate, Baldur's Gate, and Basilisk Gate. Gateway Plaza and Thran Portal aren't at their best in a two-color deck, so omitting those leaves him with seven Gates in the deck, a perfect match for the seven bridges of Königsberg. He's thrown in a Mosswort Bridge too, as an homage to the original setting of the problem, not to mention working nicely with the high-power theme of his deck.
In Catherine's Court (1766-1783)
Leonhard Euler had a hard time in Catherine the Great's Russia.3 First, he lost the use of his eyes after a successful cataract surgery. You read that right, the surgery itself worked out fine, but infections and hard living--even in the most enlightened courts of the time--later cost him all of his vision. This slowed him down less than one might expect--by this point, Euler was an accomplished at dictating his works to a recorder or conversational partner.
Then the Great St. Petersburg fire burned down his house later that very same year; Catherine the Great, in a rare show of generosity, built him another one.
Two years later his wife died. Not the best time period for Euler4
Despite this bad time (losing one's house, spouse, and vision can hardly be considered a hit-parade of good fortune, after all), Euler was busier than ever in the mathematics department. He produced constantly, seemingly indifferent if not downright cheerful.
I'll let Gautshi have the final word on Euler:
"Leonhard Euler died from a stroke on September 18, 1783 while playing with one of his grandchildren. Formulae that he had written down on two of his large slates describing the mathematics underlying the spectacular balloon flight undertaken on June 5, 1783, by the brothers Montgolfier in Paris were found on the day of his death. Worked out and prepared for publication by his son, Johann Albrecht, they became the last article of Euler; it appeared in the 1784 volume of the Memoires. A stream of memoirs, however, all queued up at the presses of the Academy, were still to be published for nearly fifty years after Euler's death."
Leonhard Euler's full EDH deck is below!
Leonhard Euler's EDH Deck
View on ArchidektBuy this decklist from TCGplayer
View this decklist on Archidekt
- Religion played a large role in Euler's personal belief system, not dissimilar to Ramanujan, a devout Hindu, and as a child Euler was fascinated with religion before devoting himself to mathematics.
- As Serheii Plokkhy notes in his comprehensive history of Ukraine, monarchs named 'the great' fancied themselves 'enlightened monarchs' who made protestations of humanism but bonded over shared imperialist activities like, say, forcibly splitting what is now Poland between their empires. They also shared courtiers, most notably Voltaire and Euler. In one incident recorded by historian Will Cuppy, Voltaire once quipped that the only creature Frederick II ever showed gratitude to was the horse that carried him away from a particularly disastrous battle. Frederick retaliated at first by cutting Voltaire's coffee and chocolate allowance. Voltaire refused to recant and ultimately fled Frederick's court to the relative safety of Catherine's.
- This doesn't make him exceptional: most people had a hard time in Catherine the Great's Russian Empire.The list of crimes of a feudal empire is long so I won't go into it in this footnote, but suffice to say that for all of Catherine's enlightenment protestations, she ordered and undertook crimes and massacres of her own peasantry. It was in 1775 that she finally crushed the largest peasant rebellion against state power, Pugachev's uprising, which I cover in brief in my biography of Nestor Makhno as key context to understand liberatory movements in what is now Russia and Ukraine.
- Gautshi puts these three events into one tight little paragraph under the heading of 'The Glorious Final Stretch' in his paper: Leonhard Euler: His Life, the Man and His Works. It reads, in part: "A cataract in his left (good) eye, which already began to bother him in Berlin, now became increasingly worse, so that in 1771 Euler decided to undergo an operation. The operation, though successful, led to the formation of an abscess, which soon destroyed Euler's vision almost entirely. Later in the same year, his wooden house burned down during the great fire of St. Petersburg, and the almost blind Euler escaped from being burnt alive only by a heroic rescue by Peter Grimm, a workman from Basel. To ease the misfortune, the Empress granted funds to build a new house... Another heavy blow hit Euler in 1773 when his wife Katharina Gsell died. Euler remarried three years later so as not to be dependent on his children."
